-
 ‘불균일 확산’ 160년 난제 풀다
우리 연구진이 160년 넘게 풀리지 않던 불균일 확산 현상의 물리적 원인을 규명했다.
우리 대학 수리과학과 김용정 교수와 바이오및뇌공학과 최명철 교수 연구팀이 기존 확산 법칙이 하지 못했던 불균일한 환경에서 발생하는 분류 현상을 설명하는 새로운 확산 법칙과 실험적 증명을 제시해, 과학의 중요한 진전을 이뤄냈다고 2일 밝혔다.
미시적 입자들의 무작위적인 움직임이 만들어 내는 거시적 질량 이동 현상을 '확산'이라고 한다. 확산은 물리, 화학, 생물, 재료 등 자연 현상뿐만 아니라 정보, 경제, 주가 변동 등 사회 현상에 이르기까지 거의 모든 분야에서 발생하는데, 이는 무작위성(randomness)이 확산 현상의 주요 원인이기 때문이다.
1905년 아인슈타인은 확산을 브라운 운동과 결합해 분자의 무작위 행보(random walk)로 설명했고, 그 이후 균일한(homogeneous) 환경에서의 확산 이론은 완벽하게 정립됐다.
반면, 1856년 루트비히(Ludwig)는 불균일(heterogeneous)한 환경에서는 물질이 확산에 의해 섞이는 것이 아니라 오히려 분류(fractionation)되는 현상을 발견했다.
이후, 확산 이외에 다른 추가적인 대류(advection) 현상이 존재해서 분류 현상을 만드는지, 아니면 입자의 무작위 움직임에 의한 것인지에 대한 의문과 논쟁은 160여 년간 이어져 왔다.
연구팀은 ‘아인슈타인의 입자적 설명'이 불균일한 환경에서 발생하는 분류 현상을 설명할 수 있을 것이라는 가정하에 연구를 진행했다. 연구 결과, 미시적 수준에서의 무작위 행보(random walk)가 불균일한 환경에 적용되면 확산 계수 D는 전도도 K와 운동성 M으로 나뉘며 (D = KM), 이 중 운동성 M에 의해 분류 현상이 발생한다는 것을 수학적 계산과 유도로 밝혔다.
물리적 직관으로 보이지 않던 것이 수학적 계산을 통해 명확해진 것이다. 이렇게 만들어진 새로운 확산 법칙은 기존의 확산 법칙처럼 계수 D 하나로만 이루어지지 않고, 두 계수에 의해 결정되는 ‘2개 요소 확산 법칙(two-component diffusion law)'이 된다.
새로운 확산 법칙이 분류 현상을 완벽하게 설명할 수 있다면, 추가적인 대류 현상은 존재하지 않으며, 오직 입자들의 무작위 운동만으로 분류 현상이 발생한다는 것이 증명된다.
확산의 특성상, 분류 현상을 검증할 정도의 정밀도로 데이터를 측정하는 것이 KAIST 연구팀이 수행한 실험의 도전적 요소였으며, 연구팀은 이 사실을 실험으로 검증해 냈다.
김용정 교수는 "이번 연구는 공간적으로 이질적인 환경에서 확산만으로도 입자의 분류가 가능하다는 것을 입증한 중요한 발견으로 기존 확산 법칙이 설명하지 못한 현상을 정확히 해석해냈다.”고 말했다. 최명철 교수는 “향후 생명과학 및 재료과학 분야에서 새로운 분리 기술 개발에 기여할 것이며 나아가, 불균일한 환경에서의 확산 현상을 다루는 다양한 분야에서 제시된 확산 법칙이 활용될 수 있을 것으로 기대한다" 고 밝혔다.
연구팀은 후속 연구로 온도 불균일에 의한 분류 현상과 고체 내의 성분 불균일에 의한 분류 현상을 연구할 계획이다. 다양한 종류의 분류 현상이 2개 요소 확산 법칙으로 설명될 수 있음을 밝히고, 그 특성을 규명할 것을 계획하고 있다.
수리과학과 김호연 박사와 바이오및뇌공학과 이근민 박사과정생이 공동 제1 저자로, 김용정 교수와 최명철 교수가 공동 교신저자로 참여한 이번 연구는 국제학술지 '미국화학회지(Journal of American Chemical Society)'에 8월 30일 字 온라인 게재됐다.
(논문명: Fractionation by Spatially Heterogeneous Diffusion: Experiments and Two-Component Random Walk Model)
이 연구는 한국연구재단, 보건복지부, KAIST의 지원을 받아 수행됐다.
‘불균일 확산’ 160년 난제 풀다
우리 연구진이 160년 넘게 풀리지 않던 불균일 확산 현상의 물리적 원인을 규명했다.
우리 대학 수리과학과 김용정 교수와 바이오및뇌공학과 최명철 교수 연구팀이 기존 확산 법칙이 하지 못했던 불균일한 환경에서 발생하는 분류 현상을 설명하는 새로운 확산 법칙과 실험적 증명을 제시해, 과학의 중요한 진전을 이뤄냈다고 2일 밝혔다.
미시적 입자들의 무작위적인 움직임이 만들어 내는 거시적 질량 이동 현상을 '확산'이라고 한다. 확산은 물리, 화학, 생물, 재료 등 자연 현상뿐만 아니라 정보, 경제, 주가 변동 등 사회 현상에 이르기까지 거의 모든 분야에서 발생하는데, 이는 무작위성(randomness)이 확산 현상의 주요 원인이기 때문이다.
1905년 아인슈타인은 확산을 브라운 운동과 결합해 분자의 무작위 행보(random walk)로 설명했고, 그 이후 균일한(homogeneous) 환경에서의 확산 이론은 완벽하게 정립됐다.
반면, 1856년 루트비히(Ludwig)는 불균일(heterogeneous)한 환경에서는 물질이 확산에 의해 섞이는 것이 아니라 오히려 분류(fractionation)되는 현상을 발견했다.
이후, 확산 이외에 다른 추가적인 대류(advection) 현상이 존재해서 분류 현상을 만드는지, 아니면 입자의 무작위 움직임에 의한 것인지에 대한 의문과 논쟁은 160여 년간 이어져 왔다.
연구팀은 ‘아인슈타인의 입자적 설명'이 불균일한 환경에서 발생하는 분류 현상을 설명할 수 있을 것이라는 가정하에 연구를 진행했다. 연구 결과, 미시적 수준에서의 무작위 행보(random walk)가 불균일한 환경에 적용되면 확산 계수 D는 전도도 K와 운동성 M으로 나뉘며 (D = KM), 이 중 운동성 M에 의해 분류 현상이 발생한다는 것을 수학적 계산과 유도로 밝혔다.
물리적 직관으로 보이지 않던 것이 수학적 계산을 통해 명확해진 것이다. 이렇게 만들어진 새로운 확산 법칙은 기존의 확산 법칙처럼 계수 D 하나로만 이루어지지 않고, 두 계수에 의해 결정되는 ‘2개 요소 확산 법칙(two-component diffusion law)'이 된다.
새로운 확산 법칙이 분류 현상을 완벽하게 설명할 수 있다면, 추가적인 대류 현상은 존재하지 않으며, 오직 입자들의 무작위 운동만으로 분류 현상이 발생한다는 것이 증명된다.
확산의 특성상, 분류 현상을 검증할 정도의 정밀도로 데이터를 측정하는 것이 KAIST 연구팀이 수행한 실험의 도전적 요소였으며, 연구팀은 이 사실을 실험으로 검증해 냈다.
김용정 교수는 "이번 연구는 공간적으로 이질적인 환경에서 확산만으로도 입자의 분류가 가능하다는 것을 입증한 중요한 발견으로 기존 확산 법칙이 설명하지 못한 현상을 정확히 해석해냈다.”고 말했다. 최명철 교수는 “향후 생명과학 및 재료과학 분야에서 새로운 분리 기술 개발에 기여할 것이며 나아가, 불균일한 환경에서의 확산 현상을 다루는 다양한 분야에서 제시된 확산 법칙이 활용될 수 있을 것으로 기대한다" 고 밝혔다.
연구팀은 후속 연구로 온도 불균일에 의한 분류 현상과 고체 내의 성분 불균일에 의한 분류 현상을 연구할 계획이다. 다양한 종류의 분류 현상이 2개 요소 확산 법칙으로 설명될 수 있음을 밝히고, 그 특성을 규명할 것을 계획하고 있다.
수리과학과 김호연 박사와 바이오및뇌공학과 이근민 박사과정생이 공동 제1 저자로, 김용정 교수와 최명철 교수가 공동 교신저자로 참여한 이번 연구는 국제학술지 '미국화학회지(Journal of American Chemical Society)'에 8월 30일 字 온라인 게재됐다.
(논문명: Fractionation by Spatially Heterogeneous Diffusion: Experiments and Two-Component Random Walk Model)
이 연구는 한국연구재단, 보건복지부, KAIST의 지원을 받아 수행됐다.
2024.10.02
조회수 4553
-
 100큐비트급 양자컴퓨터 계산데이터 전격 공개
양자컴퓨터는 양자역학의 원리를 활용해 기존의 컴퓨터로는 풀기 어려운 계산을 할 수 있는 컴퓨터다. 양자컴퓨터는 암호 해독, 배터리 소재 개발, 신약 개발 등 다양한 분야에서 그동안 풀지 못한 난제들을 해결할 미래 기술로 주목받고 있다.
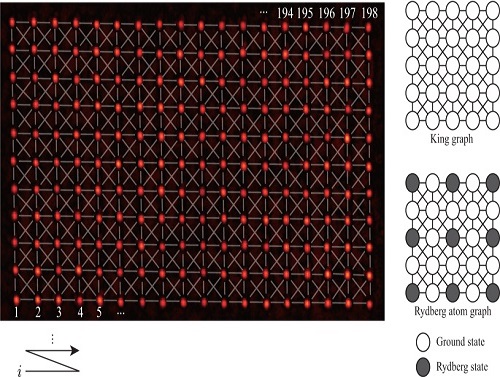
우리 대학 물리학과 안재욱 교수 연구팀이 100큐비트급 양자컴퓨터로 조합 최적화 문제를 계산해 계산 결과 데이터베이스와 계산 프로그램을 공개했다고 13일 밝혔다.
조합 최적화 문제 중 하나인 최대 독립집합 문제(Maximum independent set problem)는 SNS상에서 가장 영향력 있는 인물을 찾는 문제, 전력망을 가장 효율적으로 분배하는 법을 찾는 문제 등 다양한 응용이 가능한 문제다. 지난 2023년 KAIST 연구진은 20큐비트급 리드버그 양자컴퓨터를 이용해 최대 독립집합 문제의 풀이를 시연한 바 있다.
일반적으로 100큐비트급 양자컴퓨터의 데이터를 얻기 위해서는 직접 양자컴퓨터를 제작하거나 클라우드 서비스 업체를 이용할 수밖에 없다. 이번에 KAIST 연구진이 공개한 데이터는 관련 분야 연구자뿐 아니라 양자 컴퓨터에 관심 있는 모든 사람이 무료로 데이터에 접근할 수 있게 되었다는 점에서 중요하다고 할 수 있다. 최대 141큐비트를 활용해 70만 종류 이상의 그래프 최적화를 계산했고, 양자컴퓨터의 계산 결과와 데이터분석 프로그램 일체를 공개했다.
연구를 주도한 안재욱 교수는 “이번 연구를 통해 100큐비트급 양자컴퓨터를 활용한 난제 계산 결과 및 계산 프로그램을 모두 공개하여 그동안 양자컴퓨터에 접근이 어려웠던 연구자를 비롯한 많은 사람이 양자 컴퓨팅 연구에 참여할 수 있을 것으로 기대된다. 아울러, 고성능 양자컴퓨터 개발에 필요한 잡음 분석에도 연구팀이 계산한 데이터베이스가 활용될 수 있을 것이라 생각한다”고 말했다.
우리 대학 물리학과 김강흔, 박주영, 변우정 석박사통합과정, 김민혁 박사(現 고려대 물리학과 교수)가 참여한 해당 연구 결과는 국제 학술지 네이처(Nature) 자매지인 ‘사이언티픽 데이터(Scientific data)’1월 11권에 게재됐다. (논문명: Quantum computing dataset of maximum independent set problem on king lattice of over hundred Rydberg atoms).
한편 이번 연구는 삼성미래기술재단과 한국연구재단의 지원으로 수행됐다.
100큐비트급 양자컴퓨터 계산데이터 전격 공개
양자컴퓨터는 양자역학의 원리를 활용해 기존의 컴퓨터로는 풀기 어려운 계산을 할 수 있는 컴퓨터다. 양자컴퓨터는 암호 해독, 배터리 소재 개발, 신약 개발 등 다양한 분야에서 그동안 풀지 못한 난제들을 해결할 미래 기술로 주목받고 있다.
우리 대학 물리학과 안재욱 교수 연구팀이 100큐비트급 양자컴퓨터로 조합 최적화 문제를 계산해 계산 결과 데이터베이스와 계산 프로그램을 공개했다고 13일 밝혔다.
조합 최적화 문제 중 하나인 최대 독립집합 문제(Maximum independent set problem)는 SNS상에서 가장 영향력 있는 인물을 찾는 문제, 전력망을 가장 효율적으로 분배하는 법을 찾는 문제 등 다양한 응용이 가능한 문제다. 지난 2023년 KAIST 연구진은 20큐비트급 리드버그 양자컴퓨터를 이용해 최대 독립집합 문제의 풀이를 시연한 바 있다.
일반적으로 100큐비트급 양자컴퓨터의 데이터를 얻기 위해서는 직접 양자컴퓨터를 제작하거나 클라우드 서비스 업체를 이용할 수밖에 없다. 이번에 KAIST 연구진이 공개한 데이터는 관련 분야 연구자뿐 아니라 양자 컴퓨터에 관심 있는 모든 사람이 무료로 데이터에 접근할 수 있게 되었다는 점에서 중요하다고 할 수 있다. 최대 141큐비트를 활용해 70만 종류 이상의 그래프 최적화를 계산했고, 양자컴퓨터의 계산 결과와 데이터분석 프로그램 일체를 공개했다.
연구를 주도한 안재욱 교수는 “이번 연구를 통해 100큐비트급 양자컴퓨터를 활용한 난제 계산 결과 및 계산 프로그램을 모두 공개하여 그동안 양자컴퓨터에 접근이 어려웠던 연구자를 비롯한 많은 사람이 양자 컴퓨팅 연구에 참여할 수 있을 것으로 기대된다. 아울러, 고성능 양자컴퓨터 개발에 필요한 잡음 분석에도 연구팀이 계산한 데이터베이스가 활용될 수 있을 것이라 생각한다”고 말했다.
우리 대학 물리학과 김강흔, 박주영, 변우정 석박사통합과정, 김민혁 박사(現 고려대 물리학과 교수)가 참여한 해당 연구 결과는 국제 학술지 네이처(Nature) 자매지인 ‘사이언티픽 데이터(Scientific data)’1월 11권에 게재됐다. (논문명: Quantum computing dataset of maximum independent set problem on king lattice of over hundred Rydberg atoms).
한편 이번 연구는 삼성미래기술재단과 한국연구재단의 지원으로 수행됐다.
2024.02.13
조회수 7109
-
 4차원에서 다른 두 2차원 곡면 발견
우리 대학 수리과학과 박정환 교수가 카일 헤이든(Kyle Hayden) 콜롬비아 대학교 교수, 김승원 서울대학교 연구원, 매기 밀러(Maggie Miller) 스탠포드 대학교 연구원, 아이작 선버그(Isaac Sundberg) 막스플랑크 연구소 연구원과 함께 40년간 해결되지 않았던 위상수학계 난제를 해결했다고 5일 밝혔다.
매듭이란 3차원 공간 안에 원이 꼬여서 들어가 있는 형태를 말한다. 물리적으로는 신발 끈을 복잡하게 묶은 후에 끈의 양 끝을 하나로 붙인 원을 생각하면 된다. 매듭은 1차원적 기하학적 대상이다. 그리하여 모든 매듭은 사이퍼트 곡면이라는 2차원 곡면의 경계가 되는데 하나의 매듭이 여러 개의 서로 다른 사이퍼트 곡면의 경계가 되기도 한다. 많은 경우 위상수학에서는 하나의 차원이 더 해지면 서로 달랐던 기하학적 대상들이 같아지고는 한다. 현재 인디애나 대학교에서 명예교수로 있는 찰스 리빙스턴(Charles Livingston)은 이런 현상이 사이퍼트 곡면에서도 일어날 것이라고 1982년에 추측하였다. 즉, 그는 어떤 매듭의 두 사이퍼트 곡면이 3차원에서는 다르더라도 4차원 공간에서는 항상 같아질 것으로 추측한 것이다. 이 추측의 하나의 배경은 다년간 3차원 공간에서 다르다고 증명되었던 수많은 사이퍼트 곡면들을 많은 수학자가 4차원 공간에서 관찰하였지만, 대부분의 경우 4차원 공간에서는 같아진다는 사실을 증명하였기 때문이다.
박 교수는 동료 연구자와 함께 리빙스턴 추측이 거짓이라는 사실의 증명을 하였다. 이 증명을 포함하고 있는 ‘4차원 공안의 사이퍼트 곡면(Seifert surfaces in the 4-ball)’ 논문을 최근 프리프린트(학술지 출판 전에 사전 공개되는 논문)로 공개했다.
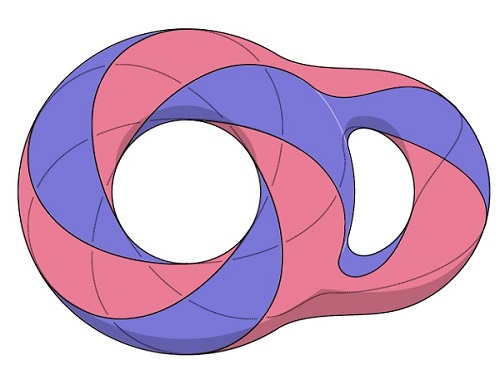
이들은 <그림 1>에서 보이는 두 개의 사이퍼트 곡면을 사용하였다. 이 두 개의 사이퍼트 곡면은 <그림 2>의 닫힌곡면을 두 개로 나누어서 얻어진 것이다. 즉, <그림 2>는 이 두 개의 사이퍼트 곡면이 같은 매듭을 경계로 한다는 사실을 설명해 주고 있다.
이 두 개의 사이퍼트 곡면이 다르다는 사실은 두 가지의 다른 방법을 사용하여 증명하였다. 첫 번째 방법은 위상수학에서 기본적으로 사용되는 피폭 공간이라는 개념을 사용하였다. 두 번째 방법은 존스 다항식(Jones polynomial)을 일반화한 코바노프 호몰로지(Khovanov homology)를 사용하였다. 특히, 위 연구자들은 코바노프 호몰로지를 이용하여 4차원 공간 안의 2차원 곡면들에 관한 다양한 연구를 진행하고 있다. 예를 들어, 이번에 발표한 논문에는 위상적으로는 4차원에서 같아지지만 매끄러운 구조를 유지하면서 같아질 수 없는 두 개의 사이퍼트 곡면의 존재성도 증명하였다. 이는 4차원 공간에서만 일어나는 미묘하고 신비한 현상을 대변한다. 박 교수와 연구자들은 이 논문은 계기로 앞으로 4차원 공간의 2차원 곡면에 대한 더 활발한 연구를 할 수 있을 것으로 기대하고 있다.
4차원에서 다른 두 2차원 곡면 발견
우리 대학 수리과학과 박정환 교수가 카일 헤이든(Kyle Hayden) 콜롬비아 대학교 교수, 김승원 서울대학교 연구원, 매기 밀러(Maggie Miller) 스탠포드 대학교 연구원, 아이작 선버그(Isaac Sundberg) 막스플랑크 연구소 연구원과 함께 40년간 해결되지 않았던 위상수학계 난제를 해결했다고 5일 밝혔다.
매듭이란 3차원 공간 안에 원이 꼬여서 들어가 있는 형태를 말한다. 물리적으로는 신발 끈을 복잡하게 묶은 후에 끈의 양 끝을 하나로 붙인 원을 생각하면 된다. 매듭은 1차원적 기하학적 대상이다. 그리하여 모든 매듭은 사이퍼트 곡면이라는 2차원 곡면의 경계가 되는데 하나의 매듭이 여러 개의 서로 다른 사이퍼트 곡면의 경계가 되기도 한다. 많은 경우 위상수학에서는 하나의 차원이 더 해지면 서로 달랐던 기하학적 대상들이 같아지고는 한다. 현재 인디애나 대학교에서 명예교수로 있는 찰스 리빙스턴(Charles Livingston)은 이런 현상이 사이퍼트 곡면에서도 일어날 것이라고 1982년에 추측하였다. 즉, 그는 어떤 매듭의 두 사이퍼트 곡면이 3차원에서는 다르더라도 4차원 공간에서는 항상 같아질 것으로 추측한 것이다. 이 추측의 하나의 배경은 다년간 3차원 공간에서 다르다고 증명되었던 수많은 사이퍼트 곡면들을 많은 수학자가 4차원 공간에서 관찰하였지만, 대부분의 경우 4차원 공간에서는 같아진다는 사실을 증명하였기 때문이다.
박 교수는 동료 연구자와 함께 리빙스턴 추측이 거짓이라는 사실의 증명을 하였다. 이 증명을 포함하고 있는 ‘4차원 공안의 사이퍼트 곡면(Seifert surfaces in the 4-ball)’ 논문을 최근 프리프린트(학술지 출판 전에 사전 공개되는 논문)로 공개했다.
이들은 <그림 1>에서 보이는 두 개의 사이퍼트 곡면을 사용하였다. 이 두 개의 사이퍼트 곡면은 <그림 2>의 닫힌곡면을 두 개로 나누어서 얻어진 것이다. 즉, <그림 2>는 이 두 개의 사이퍼트 곡면이 같은 매듭을 경계로 한다는 사실을 설명해 주고 있다.
이 두 개의 사이퍼트 곡면이 다르다는 사실은 두 가지의 다른 방법을 사용하여 증명하였다. 첫 번째 방법은 위상수학에서 기본적으로 사용되는 피폭 공간이라는 개념을 사용하였다. 두 번째 방법은 존스 다항식(Jones polynomial)을 일반화한 코바노프 호몰로지(Khovanov homology)를 사용하였다. 특히, 위 연구자들은 코바노프 호몰로지를 이용하여 4차원 공간 안의 2차원 곡면들에 관한 다양한 연구를 진행하고 있다. 예를 들어, 이번에 발표한 논문에는 위상적으로는 4차원에서 같아지지만 매끄러운 구조를 유지하면서 같아질 수 없는 두 개의 사이퍼트 곡면의 존재성도 증명하였다. 이는 4차원 공간에서만 일어나는 미묘하고 신비한 현상을 대변한다. 박 교수와 연구자들은 이 논문은 계기로 앞으로 4차원 공간의 2차원 곡면에 대한 더 활발한 연구를 할 수 있을 것으로 기대하고 있다.
2022.07.05
조회수 6966
-
 마찰전기의 발생 원리를 세계 최초로 규명
우리 대학 물리학과 김용현 교수 연구팀이 수천 년 동안 해결되지 않은 난제 중의 난제로 알려진 마찰전기 발생 원리를 세계 최초로 규명했다고 26일 밝혔다.
김 교수 연구팀은 두 물질을 마찰시킬 때 경계면에서 발생하는 열에 의해 전하가 이동할 수 있다는 아이디어를 바탕으로 `제1 원리 전자구조 계산'과 `열전달 방정식'을 풀어 마찰전기의 미시적 작동원리를 찾아냈고, 기존에 알려진 실험적 사실을 정성적으로 기술할 수 있었을 뿐만 아니라 정량적으로도 이동 전하량을 설명해 낼 수 있었다. 기존에는 정량적으로 마찰전기를 설명할 수 있는 이론은 없었다.
마찰전기에 대한 새로운 이론은 최근 주목받고 있는 에너지 수확 기술 중의 하나인 마찰전기 나노 발전기(triboelectric nanogenerator, TENG) 효율의 혁신적 증대에 이바지할 것이며, 여러 실생활 및 반도체 산업에서 원하지 않는 문제를 일으키거나 터치스크린처럼 긍정적으로 사용되고 있는 정전기의 미시적 제어를 가능하게 할 것으로 기대된다.
물리학과 신의철 박사과정이 제1 저자로 참여하고 한국표준과학연구원 여호기 박사가 공동연구로 참여한 이번 연구는 1년여의 동료심사를 거쳐 미국물리학회 오픈엑세스 국제 학술지 `피지컬 리뷰 리서치 (Physical Review Research)' 5월 4권 2호에 지난 17일 출판됐다. (논문명 : Derivation of a governing rule in triboelectric charging and series from thermoelectricity).
마찰전기는 2,600년 전 인류가 처음 `전기'를 인식하게 된 계기로 알려질 만큼 인류와 함께한 역사가 굉장히 오래된 현상이다. 최근에는 에너지 수확 기술 중 하나로 중요하게 여겨지고 있을 뿐만 아니라 코로나19의 감염을 막기 위한 마스크 그리고 공기 정화 기술로 광범위하게 사용되고 있다.
실생활에서도 번개나 정전기 등으로 매우 친숙한 자연현상이지만 지금까지 마찰전기의 발생을 정량적으로 설명할 수 있는 양자역학 이론이나 나노기술 이론은 없었다.
김용현 교수와 여호기 박사는 2014년 열전 영상 측정 기술을 개발하며 두 물질 간의 계면에 급격한 온도변화가 발생할 수 있다는 사실에 주목했다. 계면에 마찰에 의한 열이 발생하면 열전효과에 의해 전하가 이동할 수 있고, 마찰전기의 원리를 규명할 수 있는 실마리를 찾은 것으로 기대했다. 하지만 당시 2~3명의 박사과정 학생이 달려들어도 문제는 쉽게 해결되지 않았고, 7년여 만인 지금 대부분 난관을 해결하고 마침내 마찰전기의 비밀을 인류 최초로 맛볼 수 있었다.
연구팀은 마찰전기의 전하 이동 방향을 예측할 수 있는 `마찰전기 팩터(triboelectric factor)' 공식을 유도했으며 이를 이용해서 세계 최초의 이론 마찰 대전열을 구성했다. 마찰전기 팩터는 제벡 계수(단위 온도차에서 유도되는 전압), 밀도, 비열, 열전도도 등 물질 특성으로 구성돼 있다. 또한 마찰전기로 발생시킬 수 있는 전압강하의 크기를 예측하는 `마찰전기 파워(triboelectric power)'라는 물리량 K도 연구팀이 최초로 제안했다.
마찰 대전열은 중학교 2학년 교과서에서 다루는 내용이었지만 2015년 개정 교육과정 교과서에서는 더이상 다루고 있지 않다. 기존의 경험적 방법으로 결정되는 마찰 대전열이 연구자마다 다른 결과를 보고하고 있어 부정확하다는 인식이 확산됐기 때문이다. 그러나 우리 연구팀이 미시적, 양자역학적으로 정의된 마찰전기 팩터를 이용해 정량적인 대전열을 최초로 구성했기 때문에 다시 교과서에 마찰 대전열이 실릴 수 있는 계기가 마련됐다.
김용현 교수는 "미시세계에서의 열전현상을 양자역학적으로 연구하고 있었기 때문에 인류의 난제인 마찰전기 문제를 해결할 수 있는 행운이 따랐고, 오랫동안 포기하지 않고 매달려 준 학생들과 동료들에게 감사하다ˮ 라며 "마찰전기에 대한 미시적 이해를 통해, 보다 고효율 마찰전기 나노 발전기를 물질 수준에서 설계할 수 있게 됐으며, 실생활이나 산업에서 정전기를 제어하는 데 널리 이용되기를 바란다ˮ 라고 말했다.
한편 이번 연구는 한국연구재단의 자율운영 중점연구소 지원사업, SRC 이공분야기초연구사업, 미래소재디스커버리사업, 그리고 KAIST의 최장 30년까지 지원하는 그랜드 챌린지 30 사업의 지원을 받아 수행됐고, 관련 기술은 국내 특허출원이 완료됐다.
마찰전기의 발생 원리를 세계 최초로 규명
우리 대학 물리학과 김용현 교수 연구팀이 수천 년 동안 해결되지 않은 난제 중의 난제로 알려진 마찰전기 발생 원리를 세계 최초로 규명했다고 26일 밝혔다.
김 교수 연구팀은 두 물질을 마찰시킬 때 경계면에서 발생하는 열에 의해 전하가 이동할 수 있다는 아이디어를 바탕으로 `제1 원리 전자구조 계산'과 `열전달 방정식'을 풀어 마찰전기의 미시적 작동원리를 찾아냈고, 기존에 알려진 실험적 사실을 정성적으로 기술할 수 있었을 뿐만 아니라 정량적으로도 이동 전하량을 설명해 낼 수 있었다. 기존에는 정량적으로 마찰전기를 설명할 수 있는 이론은 없었다.
마찰전기에 대한 새로운 이론은 최근 주목받고 있는 에너지 수확 기술 중의 하나인 마찰전기 나노 발전기(triboelectric nanogenerator, TENG) 효율의 혁신적 증대에 이바지할 것이며, 여러 실생활 및 반도체 산업에서 원하지 않는 문제를 일으키거나 터치스크린처럼 긍정적으로 사용되고 있는 정전기의 미시적 제어를 가능하게 할 것으로 기대된다.
물리학과 신의철 박사과정이 제1 저자로 참여하고 한국표준과학연구원 여호기 박사가 공동연구로 참여한 이번 연구는 1년여의 동료심사를 거쳐 미국물리학회 오픈엑세스 국제 학술지 `피지컬 리뷰 리서치 (Physical Review Research)' 5월 4권 2호에 지난 17일 출판됐다. (논문명 : Derivation of a governing rule in triboelectric charging and series from thermoelectricity).
마찰전기는 2,600년 전 인류가 처음 `전기'를 인식하게 된 계기로 알려질 만큼 인류와 함께한 역사가 굉장히 오래된 현상이다. 최근에는 에너지 수확 기술 중 하나로 중요하게 여겨지고 있을 뿐만 아니라 코로나19의 감염을 막기 위한 마스크 그리고 공기 정화 기술로 광범위하게 사용되고 있다.
실생활에서도 번개나 정전기 등으로 매우 친숙한 자연현상이지만 지금까지 마찰전기의 발생을 정량적으로 설명할 수 있는 양자역학 이론이나 나노기술 이론은 없었다.
김용현 교수와 여호기 박사는 2014년 열전 영상 측정 기술을 개발하며 두 물질 간의 계면에 급격한 온도변화가 발생할 수 있다는 사실에 주목했다. 계면에 마찰에 의한 열이 발생하면 열전효과에 의해 전하가 이동할 수 있고, 마찰전기의 원리를 규명할 수 있는 실마리를 찾은 것으로 기대했다. 하지만 당시 2~3명의 박사과정 학생이 달려들어도 문제는 쉽게 해결되지 않았고, 7년여 만인 지금 대부분 난관을 해결하고 마침내 마찰전기의 비밀을 인류 최초로 맛볼 수 있었다.
연구팀은 마찰전기의 전하 이동 방향을 예측할 수 있는 `마찰전기 팩터(triboelectric factor)' 공식을 유도했으며 이를 이용해서 세계 최초의 이론 마찰 대전열을 구성했다. 마찰전기 팩터는 제벡 계수(단위 온도차에서 유도되는 전압), 밀도, 비열, 열전도도 등 물질 특성으로 구성돼 있다. 또한 마찰전기로 발생시킬 수 있는 전압강하의 크기를 예측하는 `마찰전기 파워(triboelectric power)'라는 물리량 K도 연구팀이 최초로 제안했다.
마찰 대전열은 중학교 2학년 교과서에서 다루는 내용이었지만 2015년 개정 교육과정 교과서에서는 더이상 다루고 있지 않다. 기존의 경험적 방법으로 결정되는 마찰 대전열이 연구자마다 다른 결과를 보고하고 있어 부정확하다는 인식이 확산됐기 때문이다. 그러나 우리 연구팀이 미시적, 양자역학적으로 정의된 마찰전기 팩터를 이용해 정량적인 대전열을 최초로 구성했기 때문에 다시 교과서에 마찰 대전열이 실릴 수 있는 계기가 마련됐다.
김용현 교수는 "미시세계에서의 열전현상을 양자역학적으로 연구하고 있었기 때문에 인류의 난제인 마찰전기 문제를 해결할 수 있는 행운이 따랐고, 오랫동안 포기하지 않고 매달려 준 학생들과 동료들에게 감사하다ˮ 라며 "마찰전기에 대한 미시적 이해를 통해, 보다 고효율 마찰전기 나노 발전기를 물질 수준에서 설계할 수 있게 됐으며, 실생활이나 산업에서 정전기를 제어하는 데 널리 이용되기를 바란다ˮ 라고 말했다.
한편 이번 연구는 한국연구재단의 자율운영 중점연구소 지원사업, SRC 이공분야기초연구사업, 미래소재디스커버리사업, 그리고 KAIST의 최장 30년까지 지원하는 그랜드 챌린지 30 사업의 지원을 받아 수행됐고, 관련 기술은 국내 특허출원이 완료됐다.
2022.05.26
조회수 15736
-
 70년 만에 준-페르미 준위 분리 현상 제1 원리적으로 규명
국내 연구진이 70년 난제로 꼽히던 준-페르미 준위 분리 현상의 원자 수준 규명에 성공했다.
우리 대학 전기및전자공학부 김용훈 교수 연구팀이 반도체 소자 동작의 기원인 준-페르미 준위(quasi-Fermi level) 분리 현상을 제1 원리적으로 기술하는 데 최초로 성공했다고 27일 밝혔다.
제1 원리적인 방법이란 실험적 데이터나 경험적 모델을 사용하지 않고 슈뢰딩거 방정식을 직접 푸는 양자역학적 물질 시뮬레이션 방법이다.
김용훈 교수 연구팀의 연구 결과는 특히 비평형 상태의 나노 소자 내에서 발생하는 복잡한 전압 강하의 기원을 새로운 이론 체계와 슈퍼컴퓨터를 통해 규명함으로써, 다양한 첨단 반도체 소자의 분석 및 차세대 나노 소자 개발을 위한 이론적 틀을 제공할 것으로 기대되고 있다.
이주호 박사과정 학생이 제1 저자로 참여한 이번 연구 성과는 국제학술지 미국‘국립과학원회보(Proceedings of the National Academy of Sciences)’ 4월 23일 字 온라인판에 게재됐다. (논문명: Quasi-Fermi level splitting in nanoscale junctions from ab initio)
반도체 관련 교과서에도 소개되고 있는 준-페르미 준위 개념은 반도체 소자 내 전압인가 상황을 기술하는 표준적인 이론 도구로서 그동안 트랜지스터, 태양전지, 발광다이오드(LED) 등 다양한 반도체 소자들의 구동 원리를 이해하거나 성능을 결정하는데 경험적으로 사용돼왔다.
하지만 준-페르미 준위 분포 현상은 1956년 노벨 물리학상 수상자 윌리엄 쇼클리(William B. Shockley)가 제시한 지 70년이 지난 현재에도 전압 인가 상황의 반도체 소자 채널 내에서 측정을 하거나 계산을 해야 하는 어려움 때문에 원자 수준에서는 이해되지 못한 상황이 계속돼왔다.
연구팀은 차세대 반도체 소자의 후보군으로 주목을 받는 단일분자 소자에서, 나노미터 길이에서 발생하는 복잡한 전압 강하 현상을 최초로 규명해냈다. 특히 전도성이 강한 특정 나노 전자소자에 대해 비 선형적 전압 강하 현상이 일어나는 원인이 준-페르미 준위 분리 현상임을 밝혔다.
이러한 연구 성과는 김 교수 연구팀이 다년간에 걸쳐 새로운 반도체 소자 제1 원리 계산 이론을 확립하고 이를 소프트웨어적으로 구현했기에 가능했다. 이는 외산 소프트웨어에만 의존하던 반도체 설계 분야에서 세계적으로 경쟁력 있는 차세대 나노소자 전산 설계 원천기술을 확보했다는 점에서 큰 의미를 부여할 수 있다.
한편 이번 연구는 과학기술정보통신부 중견연구자지원사업, 나노소재원천기술개발사업, 기초연구실지원사업, 글로벌프론티어사업의 지원을 받아 수행됐다.
70년 만에 준-페르미 준위 분리 현상 제1 원리적으로 규명
국내 연구진이 70년 난제로 꼽히던 준-페르미 준위 분리 현상의 원자 수준 규명에 성공했다.
우리 대학 전기및전자공학부 김용훈 교수 연구팀이 반도체 소자 동작의 기원인 준-페르미 준위(quasi-Fermi level) 분리 현상을 제1 원리적으로 기술하는 데 최초로 성공했다고 27일 밝혔다.
제1 원리적인 방법이란 실험적 데이터나 경험적 모델을 사용하지 않고 슈뢰딩거 방정식을 직접 푸는 양자역학적 물질 시뮬레이션 방법이다.
김용훈 교수 연구팀의 연구 결과는 특히 비평형 상태의 나노 소자 내에서 발생하는 복잡한 전압 강하의 기원을 새로운 이론 체계와 슈퍼컴퓨터를 통해 규명함으로써, 다양한 첨단 반도체 소자의 분석 및 차세대 나노 소자 개발을 위한 이론적 틀을 제공할 것으로 기대되고 있다.
이주호 박사과정 학생이 제1 저자로 참여한 이번 연구 성과는 국제학술지 미국‘국립과학원회보(Proceedings of the National Academy of Sciences)’ 4월 23일 字 온라인판에 게재됐다. (논문명: Quasi-Fermi level splitting in nanoscale junctions from ab initio)
반도체 관련 교과서에도 소개되고 있는 준-페르미 준위 개념은 반도체 소자 내 전압인가 상황을 기술하는 표준적인 이론 도구로서 그동안 트랜지스터, 태양전지, 발광다이오드(LED) 등 다양한 반도체 소자들의 구동 원리를 이해하거나 성능을 결정하는데 경험적으로 사용돼왔다.
하지만 준-페르미 준위 분포 현상은 1956년 노벨 물리학상 수상자 윌리엄 쇼클리(William B. Shockley)가 제시한 지 70년이 지난 현재에도 전압 인가 상황의 반도체 소자 채널 내에서 측정을 하거나 계산을 해야 하는 어려움 때문에 원자 수준에서는 이해되지 못한 상황이 계속돼왔다.
연구팀은 차세대 반도체 소자의 후보군으로 주목을 받는 단일분자 소자에서, 나노미터 길이에서 발생하는 복잡한 전압 강하 현상을 최초로 규명해냈다. 특히 전도성이 강한 특정 나노 전자소자에 대해 비 선형적 전압 강하 현상이 일어나는 원인이 준-페르미 준위 분리 현상임을 밝혔다.
이러한 연구 성과는 김 교수 연구팀이 다년간에 걸쳐 새로운 반도체 소자 제1 원리 계산 이론을 확립하고 이를 소프트웨어적으로 구현했기에 가능했다. 이는 외산 소프트웨어에만 의존하던 반도체 설계 분야에서 세계적으로 경쟁력 있는 차세대 나노소자 전산 설계 원천기술을 확보했다는 점에서 큰 의미를 부여할 수 있다.
한편 이번 연구는 과학기술정보통신부 중견연구자지원사업, 나노소재원천기술개발사업, 기초연구실지원사업, 글로벌프론티어사업의 지원을 받아 수행됐다.
2020.04.27
조회수 18069
 ‘불균일 확산’ 160년 난제 풀다
우리 연구진이 160년 넘게 풀리지 않던 불균일 확산 현상의 물리적 원인을 규명했다.
우리 대학 수리과학과 김용정 교수와 바이오및뇌공학과 최명철 교수 연구팀이 기존 확산 법칙이 하지 못했던 불균일한 환경에서 발생하는 분류 현상을 설명하는 새로운 확산 법칙과 실험적 증명을 제시해, 과학의 중요한 진전을 이뤄냈다고 2일 밝혔다.
미시적 입자들의 무작위적인 움직임이 만들어 내는 거시적 질량 이동 현상을 '확산'이라고 한다. 확산은 물리, 화학, 생물, 재료 등 자연 현상뿐만 아니라 정보, 경제, 주가 변동 등 사회 현상에 이르기까지 거의 모든 분야에서 발생하는데, 이는 무작위성(randomness)이 확산 현상의 주요 원인이기 때문이다.
1905년 아인슈타인은 확산을 브라운 운동과 결합해 분자의 무작위 행보(random walk)로 설명했고, 그 이후 균일한(homogeneous) 환경에서의 확산 이론은 완벽하게 정립됐다.
반면, 1856년 루트비히(Ludwig)는 불균일(heterogeneous)한 환경에서는 물질이 확산에 의해 섞이는 것이 아니라 오히려 분류(fractionation)되는 현상을 발견했다.
이후, 확산 이외에 다른 추가적인 대류(advection) 현상이 존재해서 분류 현상을 만드는지, 아니면 입자의 무작위 움직임에 의한 것인지에 대한 의문과 논쟁은 160여 년간 이어져 왔다.
연구팀은 ‘아인슈타인의 입자적 설명'이 불균일한 환경에서 발생하는 분류 현상을 설명할 수 있을 것이라는 가정하에 연구를 진행했다. 연구 결과, 미시적 수준에서의 무작위 행보(random walk)가 불균일한 환경에 적용되면 확산 계수 D는 전도도 K와 운동성 M으로 나뉘며 (D = KM), 이 중 운동성 M에 의해 분류 현상이 발생한다는 것을 수학적 계산과 유도로 밝혔다.
물리적 직관으로 보이지 않던 것이 수학적 계산을 통해 명확해진 것이다. 이렇게 만들어진 새로운 확산 법칙은 기존의 확산 법칙처럼 계수 D 하나로만 이루어지지 않고, 두 계수에 의해 결정되는 ‘2개 요소 확산 법칙(two-component diffusion law)'이 된다.
새로운 확산 법칙이 분류 현상을 완벽하게 설명할 수 있다면, 추가적인 대류 현상은 존재하지 않으며, 오직 입자들의 무작위 운동만으로 분류 현상이 발생한다는 것이 증명된다.
확산의 특성상, 분류 현상을 검증할 정도의 정밀도로 데이터를 측정하는 것이 KAIST 연구팀이 수행한 실험의 도전적 요소였으며, 연구팀은 이 사실을 실험으로 검증해 냈다.
김용정 교수는 "이번 연구는 공간적으로 이질적인 환경에서 확산만으로도 입자의 분류가 가능하다는 것을 입증한 중요한 발견으로 기존 확산 법칙이 설명하지 못한 현상을 정확히 해석해냈다.”고 말했다. 최명철 교수는 “향후 생명과학 및 재료과학 분야에서 새로운 분리 기술 개발에 기여할 것이며 나아가, 불균일한 환경에서의 확산 현상을 다루는 다양한 분야에서 제시된 확산 법칙이 활용될 수 있을 것으로 기대한다" 고 밝혔다.
연구팀은 후속 연구로 온도 불균일에 의한 분류 현상과 고체 내의 성분 불균일에 의한 분류 현상을 연구할 계획이다. 다양한 종류의 분류 현상이 2개 요소 확산 법칙으로 설명될 수 있음을 밝히고, 그 특성을 규명할 것을 계획하고 있다.
수리과학과 김호연 박사와 바이오및뇌공학과 이근민 박사과정생이 공동 제1 저자로, 김용정 교수와 최명철 교수가 공동 교신저자로 참여한 이번 연구는 국제학술지 '미국화학회지(Journal of American Chemical Society)'에 8월 30일 字 온라인 게재됐다.
(논문명: Fractionation by Spatially Heterogeneous Diffusion: Experiments and Two-Component Random Walk Model)
이 연구는 한국연구재단, 보건복지부, KAIST의 지원을 받아 수행됐다.
2024.10.02 조회수 4553
‘불균일 확산’ 160년 난제 풀다
우리 연구진이 160년 넘게 풀리지 않던 불균일 확산 현상의 물리적 원인을 규명했다.
우리 대학 수리과학과 김용정 교수와 바이오및뇌공학과 최명철 교수 연구팀이 기존 확산 법칙이 하지 못했던 불균일한 환경에서 발생하는 분류 현상을 설명하는 새로운 확산 법칙과 실험적 증명을 제시해, 과학의 중요한 진전을 이뤄냈다고 2일 밝혔다.
미시적 입자들의 무작위적인 움직임이 만들어 내는 거시적 질량 이동 현상을 '확산'이라고 한다. 확산은 물리, 화학, 생물, 재료 등 자연 현상뿐만 아니라 정보, 경제, 주가 변동 등 사회 현상에 이르기까지 거의 모든 분야에서 발생하는데, 이는 무작위성(randomness)이 확산 현상의 주요 원인이기 때문이다.
1905년 아인슈타인은 확산을 브라운 운동과 결합해 분자의 무작위 행보(random walk)로 설명했고, 그 이후 균일한(homogeneous) 환경에서의 확산 이론은 완벽하게 정립됐다.
반면, 1856년 루트비히(Ludwig)는 불균일(heterogeneous)한 환경에서는 물질이 확산에 의해 섞이는 것이 아니라 오히려 분류(fractionation)되는 현상을 발견했다.
이후, 확산 이외에 다른 추가적인 대류(advection) 현상이 존재해서 분류 현상을 만드는지, 아니면 입자의 무작위 움직임에 의한 것인지에 대한 의문과 논쟁은 160여 년간 이어져 왔다.
연구팀은 ‘아인슈타인의 입자적 설명'이 불균일한 환경에서 발생하는 분류 현상을 설명할 수 있을 것이라는 가정하에 연구를 진행했다. 연구 결과, 미시적 수준에서의 무작위 행보(random walk)가 불균일한 환경에 적용되면 확산 계수 D는 전도도 K와 운동성 M으로 나뉘며 (D = KM), 이 중 운동성 M에 의해 분류 현상이 발생한다는 것을 수학적 계산과 유도로 밝혔다.
물리적 직관으로 보이지 않던 것이 수학적 계산을 통해 명확해진 것이다. 이렇게 만들어진 새로운 확산 법칙은 기존의 확산 법칙처럼 계수 D 하나로만 이루어지지 않고, 두 계수에 의해 결정되는 ‘2개 요소 확산 법칙(two-component diffusion law)'이 된다.
새로운 확산 법칙이 분류 현상을 완벽하게 설명할 수 있다면, 추가적인 대류 현상은 존재하지 않으며, 오직 입자들의 무작위 운동만으로 분류 현상이 발생한다는 것이 증명된다.
확산의 특성상, 분류 현상을 검증할 정도의 정밀도로 데이터를 측정하는 것이 KAIST 연구팀이 수행한 실험의 도전적 요소였으며, 연구팀은 이 사실을 실험으로 검증해 냈다.
김용정 교수는 "이번 연구는 공간적으로 이질적인 환경에서 확산만으로도 입자의 분류가 가능하다는 것을 입증한 중요한 발견으로 기존 확산 법칙이 설명하지 못한 현상을 정확히 해석해냈다.”고 말했다. 최명철 교수는 “향후 생명과학 및 재료과학 분야에서 새로운 분리 기술 개발에 기여할 것이며 나아가, 불균일한 환경에서의 확산 현상을 다루는 다양한 분야에서 제시된 확산 법칙이 활용될 수 있을 것으로 기대한다" 고 밝혔다.
연구팀은 후속 연구로 온도 불균일에 의한 분류 현상과 고체 내의 성분 불균일에 의한 분류 현상을 연구할 계획이다. 다양한 종류의 분류 현상이 2개 요소 확산 법칙으로 설명될 수 있음을 밝히고, 그 특성을 규명할 것을 계획하고 있다.
수리과학과 김호연 박사와 바이오및뇌공학과 이근민 박사과정생이 공동 제1 저자로, 김용정 교수와 최명철 교수가 공동 교신저자로 참여한 이번 연구는 국제학술지 '미국화학회지(Journal of American Chemical Society)'에 8월 30일 字 온라인 게재됐다.
(논문명: Fractionation by Spatially Heterogeneous Diffusion: Experiments and Two-Component Random Walk Model)
이 연구는 한국연구재단, 보건복지부, KAIST의 지원을 받아 수행됐다.
2024.10.02 조회수 4553 100큐비트급 양자컴퓨터 계산데이터 전격 공개
양자컴퓨터는 양자역학의 원리를 활용해 기존의 컴퓨터로는 풀기 어려운 계산을 할 수 있는 컴퓨터다. 양자컴퓨터는 암호 해독, 배터리 소재 개발, 신약 개발 등 다양한 분야에서 그동안 풀지 못한 난제들을 해결할 미래 기술로 주목받고 있다.
우리 대학 물리학과 안재욱 교수 연구팀이 100큐비트급 양자컴퓨터로 조합 최적화 문제를 계산해 계산 결과 데이터베이스와 계산 프로그램을 공개했다고 13일 밝혔다.
조합 최적화 문제 중 하나인 최대 독립집합 문제(Maximum independent set problem)는 SNS상에서 가장 영향력 있는 인물을 찾는 문제, 전력망을 가장 효율적으로 분배하는 법을 찾는 문제 등 다양한 응용이 가능한 문제다. 지난 2023년 KAIST 연구진은 20큐비트급 리드버그 양자컴퓨터를 이용해 최대 독립집합 문제의 풀이를 시연한 바 있다.
일반적으로 100큐비트급 양자컴퓨터의 데이터를 얻기 위해서는 직접 양자컴퓨터를 제작하거나 클라우드 서비스 업체를 이용할 수밖에 없다. 이번에 KAIST 연구진이 공개한 데이터는 관련 분야 연구자뿐 아니라 양자 컴퓨터에 관심 있는 모든 사람이 무료로 데이터에 접근할 수 있게 되었다는 점에서 중요하다고 할 수 있다. 최대 141큐비트를 활용해 70만 종류 이상의 그래프 최적화를 계산했고, 양자컴퓨터의 계산 결과와 데이터분석 프로그램 일체를 공개했다.
연구를 주도한 안재욱 교수는 “이번 연구를 통해 100큐비트급 양자컴퓨터를 활용한 난제 계산 결과 및 계산 프로그램을 모두 공개하여 그동안 양자컴퓨터에 접근이 어려웠던 연구자를 비롯한 많은 사람이 양자 컴퓨팅 연구에 참여할 수 있을 것으로 기대된다. 아울러, 고성능 양자컴퓨터 개발에 필요한 잡음 분석에도 연구팀이 계산한 데이터베이스가 활용될 수 있을 것이라 생각한다”고 말했다.
우리 대학 물리학과 김강흔, 박주영, 변우정 석박사통합과정, 김민혁 박사(現 고려대 물리학과 교수)가 참여한 해당 연구 결과는 국제 학술지 네이처(Nature) 자매지인 ‘사이언티픽 데이터(Scientific data)’1월 11권에 게재됐다. (논문명: Quantum computing dataset of maximum independent set problem on king lattice of over hundred Rydberg atoms).
한편 이번 연구는 삼성미래기술재단과 한국연구재단의 지원으로 수행됐다.
2024.02.13 조회수 7109
100큐비트급 양자컴퓨터 계산데이터 전격 공개
양자컴퓨터는 양자역학의 원리를 활용해 기존의 컴퓨터로는 풀기 어려운 계산을 할 수 있는 컴퓨터다. 양자컴퓨터는 암호 해독, 배터리 소재 개발, 신약 개발 등 다양한 분야에서 그동안 풀지 못한 난제들을 해결할 미래 기술로 주목받고 있다.
우리 대학 물리학과 안재욱 교수 연구팀이 100큐비트급 양자컴퓨터로 조합 최적화 문제를 계산해 계산 결과 데이터베이스와 계산 프로그램을 공개했다고 13일 밝혔다.
조합 최적화 문제 중 하나인 최대 독립집합 문제(Maximum independent set problem)는 SNS상에서 가장 영향력 있는 인물을 찾는 문제, 전력망을 가장 효율적으로 분배하는 법을 찾는 문제 등 다양한 응용이 가능한 문제다. 지난 2023년 KAIST 연구진은 20큐비트급 리드버그 양자컴퓨터를 이용해 최대 독립집합 문제의 풀이를 시연한 바 있다.
일반적으로 100큐비트급 양자컴퓨터의 데이터를 얻기 위해서는 직접 양자컴퓨터를 제작하거나 클라우드 서비스 업체를 이용할 수밖에 없다. 이번에 KAIST 연구진이 공개한 데이터는 관련 분야 연구자뿐 아니라 양자 컴퓨터에 관심 있는 모든 사람이 무료로 데이터에 접근할 수 있게 되었다는 점에서 중요하다고 할 수 있다. 최대 141큐비트를 활용해 70만 종류 이상의 그래프 최적화를 계산했고, 양자컴퓨터의 계산 결과와 데이터분석 프로그램 일체를 공개했다.
연구를 주도한 안재욱 교수는 “이번 연구를 통해 100큐비트급 양자컴퓨터를 활용한 난제 계산 결과 및 계산 프로그램을 모두 공개하여 그동안 양자컴퓨터에 접근이 어려웠던 연구자를 비롯한 많은 사람이 양자 컴퓨팅 연구에 참여할 수 있을 것으로 기대된다. 아울러, 고성능 양자컴퓨터 개발에 필요한 잡음 분석에도 연구팀이 계산한 데이터베이스가 활용될 수 있을 것이라 생각한다”고 말했다.
우리 대학 물리학과 김강흔, 박주영, 변우정 석박사통합과정, 김민혁 박사(現 고려대 물리학과 교수)가 참여한 해당 연구 결과는 국제 학술지 네이처(Nature) 자매지인 ‘사이언티픽 데이터(Scientific data)’1월 11권에 게재됐다. (논문명: Quantum computing dataset of maximum independent set problem on king lattice of over hundred Rydberg atoms).
한편 이번 연구는 삼성미래기술재단과 한국연구재단의 지원으로 수행됐다.
2024.02.13 조회수 7109 4차원에서 다른 두 2차원 곡면 발견
우리 대학 수리과학과 박정환 교수가 카일 헤이든(Kyle Hayden) 콜롬비아 대학교 교수, 김승원 서울대학교 연구원, 매기 밀러(Maggie Miller) 스탠포드 대학교 연구원, 아이작 선버그(Isaac Sundberg) 막스플랑크 연구소 연구원과 함께 40년간 해결되지 않았던 위상수학계 난제를 해결했다고 5일 밝혔다.
매듭이란 3차원 공간 안에 원이 꼬여서 들어가 있는 형태를 말한다. 물리적으로는 신발 끈을 복잡하게 묶은 후에 끈의 양 끝을 하나로 붙인 원을 생각하면 된다. 매듭은 1차원적 기하학적 대상이다. 그리하여 모든 매듭은 사이퍼트 곡면이라는 2차원 곡면의 경계가 되는데 하나의 매듭이 여러 개의 서로 다른 사이퍼트 곡면의 경계가 되기도 한다. 많은 경우 위상수학에서는 하나의 차원이 더 해지면 서로 달랐던 기하학적 대상들이 같아지고는 한다. 현재 인디애나 대학교에서 명예교수로 있는 찰스 리빙스턴(Charles Livingston)은 이런 현상이 사이퍼트 곡면에서도 일어날 것이라고 1982년에 추측하였다. 즉, 그는 어떤 매듭의 두 사이퍼트 곡면이 3차원에서는 다르더라도 4차원 공간에서는 항상 같아질 것으로 추측한 것이다. 이 추측의 하나의 배경은 다년간 3차원 공간에서 다르다고 증명되었던 수많은 사이퍼트 곡면들을 많은 수학자가 4차원 공간에서 관찰하였지만, 대부분의 경우 4차원 공간에서는 같아진다는 사실을 증명하였기 때문이다.
박 교수는 동료 연구자와 함께 리빙스턴 추측이 거짓이라는 사실의 증명을 하였다. 이 증명을 포함하고 있는 ‘4차원 공안의 사이퍼트 곡면(Seifert surfaces in the 4-ball)’ 논문을 최근 프리프린트(학술지 출판 전에 사전 공개되는 논문)로 공개했다.
이들은 <그림 1>에서 보이는 두 개의 사이퍼트 곡면을 사용하였다. 이 두 개의 사이퍼트 곡면은 <그림 2>의 닫힌곡면을 두 개로 나누어서 얻어진 것이다. 즉, <그림 2>는 이 두 개의 사이퍼트 곡면이 같은 매듭을 경계로 한다는 사실을 설명해 주고 있다.
이 두 개의 사이퍼트 곡면이 다르다는 사실은 두 가지의 다른 방법을 사용하여 증명하였다. 첫 번째 방법은 위상수학에서 기본적으로 사용되는 피폭 공간이라는 개념을 사용하였다. 두 번째 방법은 존스 다항식(Jones polynomial)을 일반화한 코바노프 호몰로지(Khovanov homology)를 사용하였다. 특히, 위 연구자들은 코바노프 호몰로지를 이용하여 4차원 공간 안의 2차원 곡면들에 관한 다양한 연구를 진행하고 있다. 예를 들어, 이번에 발표한 논문에는 위상적으로는 4차원에서 같아지지만 매끄러운 구조를 유지하면서 같아질 수 없는 두 개의 사이퍼트 곡면의 존재성도 증명하였다. 이는 4차원 공간에서만 일어나는 미묘하고 신비한 현상을 대변한다. 박 교수와 연구자들은 이 논문은 계기로 앞으로 4차원 공간의 2차원 곡면에 대한 더 활발한 연구를 할 수 있을 것으로 기대하고 있다.
2022.07.05 조회수 6966
4차원에서 다른 두 2차원 곡면 발견
우리 대학 수리과학과 박정환 교수가 카일 헤이든(Kyle Hayden) 콜롬비아 대학교 교수, 김승원 서울대학교 연구원, 매기 밀러(Maggie Miller) 스탠포드 대학교 연구원, 아이작 선버그(Isaac Sundberg) 막스플랑크 연구소 연구원과 함께 40년간 해결되지 않았던 위상수학계 난제를 해결했다고 5일 밝혔다.
매듭이란 3차원 공간 안에 원이 꼬여서 들어가 있는 형태를 말한다. 물리적으로는 신발 끈을 복잡하게 묶은 후에 끈의 양 끝을 하나로 붙인 원을 생각하면 된다. 매듭은 1차원적 기하학적 대상이다. 그리하여 모든 매듭은 사이퍼트 곡면이라는 2차원 곡면의 경계가 되는데 하나의 매듭이 여러 개의 서로 다른 사이퍼트 곡면의 경계가 되기도 한다. 많은 경우 위상수학에서는 하나의 차원이 더 해지면 서로 달랐던 기하학적 대상들이 같아지고는 한다. 현재 인디애나 대학교에서 명예교수로 있는 찰스 리빙스턴(Charles Livingston)은 이런 현상이 사이퍼트 곡면에서도 일어날 것이라고 1982년에 추측하였다. 즉, 그는 어떤 매듭의 두 사이퍼트 곡면이 3차원에서는 다르더라도 4차원 공간에서는 항상 같아질 것으로 추측한 것이다. 이 추측의 하나의 배경은 다년간 3차원 공간에서 다르다고 증명되었던 수많은 사이퍼트 곡면들을 많은 수학자가 4차원 공간에서 관찰하였지만, 대부분의 경우 4차원 공간에서는 같아진다는 사실을 증명하였기 때문이다.
박 교수는 동료 연구자와 함께 리빙스턴 추측이 거짓이라는 사실의 증명을 하였다. 이 증명을 포함하고 있는 ‘4차원 공안의 사이퍼트 곡면(Seifert surfaces in the 4-ball)’ 논문을 최근 프리프린트(학술지 출판 전에 사전 공개되는 논문)로 공개했다.
이들은 <그림 1>에서 보이는 두 개의 사이퍼트 곡면을 사용하였다. 이 두 개의 사이퍼트 곡면은 <그림 2>의 닫힌곡면을 두 개로 나누어서 얻어진 것이다. 즉, <그림 2>는 이 두 개의 사이퍼트 곡면이 같은 매듭을 경계로 한다는 사실을 설명해 주고 있다.
이 두 개의 사이퍼트 곡면이 다르다는 사실은 두 가지의 다른 방법을 사용하여 증명하였다. 첫 번째 방법은 위상수학에서 기본적으로 사용되는 피폭 공간이라는 개념을 사용하였다. 두 번째 방법은 존스 다항식(Jones polynomial)을 일반화한 코바노프 호몰로지(Khovanov homology)를 사용하였다. 특히, 위 연구자들은 코바노프 호몰로지를 이용하여 4차원 공간 안의 2차원 곡면들에 관한 다양한 연구를 진행하고 있다. 예를 들어, 이번에 발표한 논문에는 위상적으로는 4차원에서 같아지지만 매끄러운 구조를 유지하면서 같아질 수 없는 두 개의 사이퍼트 곡면의 존재성도 증명하였다. 이는 4차원 공간에서만 일어나는 미묘하고 신비한 현상을 대변한다. 박 교수와 연구자들은 이 논문은 계기로 앞으로 4차원 공간의 2차원 곡면에 대한 더 활발한 연구를 할 수 있을 것으로 기대하고 있다.
2022.07.05 조회수 6966 마찰전기의 발생 원리를 세계 최초로 규명
우리 대학 물리학과 김용현 교수 연구팀이 수천 년 동안 해결되지 않은 난제 중의 난제로 알려진 마찰전기 발생 원리를 세계 최초로 규명했다고 26일 밝혔다.
김 교수 연구팀은 두 물질을 마찰시킬 때 경계면에서 발생하는 열에 의해 전하가 이동할 수 있다는 아이디어를 바탕으로 `제1 원리 전자구조 계산'과 `열전달 방정식'을 풀어 마찰전기의 미시적 작동원리를 찾아냈고, 기존에 알려진 실험적 사실을 정성적으로 기술할 수 있었을 뿐만 아니라 정량적으로도 이동 전하량을 설명해 낼 수 있었다. 기존에는 정량적으로 마찰전기를 설명할 수 있는 이론은 없었다.
마찰전기에 대한 새로운 이론은 최근 주목받고 있는 에너지 수확 기술 중의 하나인 마찰전기 나노 발전기(triboelectric nanogenerator, TENG) 효율의 혁신적 증대에 이바지할 것이며, 여러 실생활 및 반도체 산업에서 원하지 않는 문제를 일으키거나 터치스크린처럼 긍정적으로 사용되고 있는 정전기의 미시적 제어를 가능하게 할 것으로 기대된다.
물리학과 신의철 박사과정이 제1 저자로 참여하고 한국표준과학연구원 여호기 박사가 공동연구로 참여한 이번 연구는 1년여의 동료심사를 거쳐 미국물리학회 오픈엑세스 국제 학술지 `피지컬 리뷰 리서치 (Physical Review Research)' 5월 4권 2호에 지난 17일 출판됐다. (논문명 : Derivation of a governing rule in triboelectric charging and series from thermoelectricity).
마찰전기는 2,600년 전 인류가 처음 `전기'를 인식하게 된 계기로 알려질 만큼 인류와 함께한 역사가 굉장히 오래된 현상이다. 최근에는 에너지 수확 기술 중 하나로 중요하게 여겨지고 있을 뿐만 아니라 코로나19의 감염을 막기 위한 마스크 그리고 공기 정화 기술로 광범위하게 사용되고 있다.
실생활에서도 번개나 정전기 등으로 매우 친숙한 자연현상이지만 지금까지 마찰전기의 발생을 정량적으로 설명할 수 있는 양자역학 이론이나 나노기술 이론은 없었다.
김용현 교수와 여호기 박사는 2014년 열전 영상 측정 기술을 개발하며 두 물질 간의 계면에 급격한 온도변화가 발생할 수 있다는 사실에 주목했다. 계면에 마찰에 의한 열이 발생하면 열전효과에 의해 전하가 이동할 수 있고, 마찰전기의 원리를 규명할 수 있는 실마리를 찾은 것으로 기대했다. 하지만 당시 2~3명의 박사과정 학생이 달려들어도 문제는 쉽게 해결되지 않았고, 7년여 만인 지금 대부분 난관을 해결하고 마침내 마찰전기의 비밀을 인류 최초로 맛볼 수 있었다.
연구팀은 마찰전기의 전하 이동 방향을 예측할 수 있는 `마찰전기 팩터(triboelectric factor)' 공식을 유도했으며 이를 이용해서 세계 최초의 이론 마찰 대전열을 구성했다. 마찰전기 팩터는 제벡 계수(단위 온도차에서 유도되는 전압), 밀도, 비열, 열전도도 등 물질 특성으로 구성돼 있다. 또한 마찰전기로 발생시킬 수 있는 전압강하의 크기를 예측하는 `마찰전기 파워(triboelectric power)'라는 물리량 K도 연구팀이 최초로 제안했다.
마찰 대전열은 중학교 2학년 교과서에서 다루는 내용이었지만 2015년 개정 교육과정 교과서에서는 더이상 다루고 있지 않다. 기존의 경험적 방법으로 결정되는 마찰 대전열이 연구자마다 다른 결과를 보고하고 있어 부정확하다는 인식이 확산됐기 때문이다. 그러나 우리 연구팀이 미시적, 양자역학적으로 정의된 마찰전기 팩터를 이용해 정량적인 대전열을 최초로 구성했기 때문에 다시 교과서에 마찰 대전열이 실릴 수 있는 계기가 마련됐다.
김용현 교수는 "미시세계에서의 열전현상을 양자역학적으로 연구하고 있었기 때문에 인류의 난제인 마찰전기 문제를 해결할 수 있는 행운이 따랐고, 오랫동안 포기하지 않고 매달려 준 학생들과 동료들에게 감사하다ˮ 라며 "마찰전기에 대한 미시적 이해를 통해, 보다 고효율 마찰전기 나노 발전기를 물질 수준에서 설계할 수 있게 됐으며, 실생활이나 산업에서 정전기를 제어하는 데 널리 이용되기를 바란다ˮ 라고 말했다.
한편 이번 연구는 한국연구재단의 자율운영 중점연구소 지원사업, SRC 이공분야기초연구사업, 미래소재디스커버리사업, 그리고 KAIST의 최장 30년까지 지원하는 그랜드 챌린지 30 사업의 지원을 받아 수행됐고, 관련 기술은 국내 특허출원이 완료됐다.
2022.05.26 조회수 15736
마찰전기의 발생 원리를 세계 최초로 규명
우리 대학 물리학과 김용현 교수 연구팀이 수천 년 동안 해결되지 않은 난제 중의 난제로 알려진 마찰전기 발생 원리를 세계 최초로 규명했다고 26일 밝혔다.
김 교수 연구팀은 두 물질을 마찰시킬 때 경계면에서 발생하는 열에 의해 전하가 이동할 수 있다는 아이디어를 바탕으로 `제1 원리 전자구조 계산'과 `열전달 방정식'을 풀어 마찰전기의 미시적 작동원리를 찾아냈고, 기존에 알려진 실험적 사실을 정성적으로 기술할 수 있었을 뿐만 아니라 정량적으로도 이동 전하량을 설명해 낼 수 있었다. 기존에는 정량적으로 마찰전기를 설명할 수 있는 이론은 없었다.
마찰전기에 대한 새로운 이론은 최근 주목받고 있는 에너지 수확 기술 중의 하나인 마찰전기 나노 발전기(triboelectric nanogenerator, TENG) 효율의 혁신적 증대에 이바지할 것이며, 여러 실생활 및 반도체 산업에서 원하지 않는 문제를 일으키거나 터치스크린처럼 긍정적으로 사용되고 있는 정전기의 미시적 제어를 가능하게 할 것으로 기대된다.
물리학과 신의철 박사과정이 제1 저자로 참여하고 한국표준과학연구원 여호기 박사가 공동연구로 참여한 이번 연구는 1년여의 동료심사를 거쳐 미국물리학회 오픈엑세스 국제 학술지 `피지컬 리뷰 리서치 (Physical Review Research)' 5월 4권 2호에 지난 17일 출판됐다. (논문명 : Derivation of a governing rule in triboelectric charging and series from thermoelectricity).
마찰전기는 2,600년 전 인류가 처음 `전기'를 인식하게 된 계기로 알려질 만큼 인류와 함께한 역사가 굉장히 오래된 현상이다. 최근에는 에너지 수확 기술 중 하나로 중요하게 여겨지고 있을 뿐만 아니라 코로나19의 감염을 막기 위한 마스크 그리고 공기 정화 기술로 광범위하게 사용되고 있다.
실생활에서도 번개나 정전기 등으로 매우 친숙한 자연현상이지만 지금까지 마찰전기의 발생을 정량적으로 설명할 수 있는 양자역학 이론이나 나노기술 이론은 없었다.
김용현 교수와 여호기 박사는 2014년 열전 영상 측정 기술을 개발하며 두 물질 간의 계면에 급격한 온도변화가 발생할 수 있다는 사실에 주목했다. 계면에 마찰에 의한 열이 발생하면 열전효과에 의해 전하가 이동할 수 있고, 마찰전기의 원리를 규명할 수 있는 실마리를 찾은 것으로 기대했다. 하지만 당시 2~3명의 박사과정 학생이 달려들어도 문제는 쉽게 해결되지 않았고, 7년여 만인 지금 대부분 난관을 해결하고 마침내 마찰전기의 비밀을 인류 최초로 맛볼 수 있었다.
연구팀은 마찰전기의 전하 이동 방향을 예측할 수 있는 `마찰전기 팩터(triboelectric factor)' 공식을 유도했으며 이를 이용해서 세계 최초의 이론 마찰 대전열을 구성했다. 마찰전기 팩터는 제벡 계수(단위 온도차에서 유도되는 전압), 밀도, 비열, 열전도도 등 물질 특성으로 구성돼 있다. 또한 마찰전기로 발생시킬 수 있는 전압강하의 크기를 예측하는 `마찰전기 파워(triboelectric power)'라는 물리량 K도 연구팀이 최초로 제안했다.
마찰 대전열은 중학교 2학년 교과서에서 다루는 내용이었지만 2015년 개정 교육과정 교과서에서는 더이상 다루고 있지 않다. 기존의 경험적 방법으로 결정되는 마찰 대전열이 연구자마다 다른 결과를 보고하고 있어 부정확하다는 인식이 확산됐기 때문이다. 그러나 우리 연구팀이 미시적, 양자역학적으로 정의된 마찰전기 팩터를 이용해 정량적인 대전열을 최초로 구성했기 때문에 다시 교과서에 마찰 대전열이 실릴 수 있는 계기가 마련됐다.
김용현 교수는 "미시세계에서의 열전현상을 양자역학적으로 연구하고 있었기 때문에 인류의 난제인 마찰전기 문제를 해결할 수 있는 행운이 따랐고, 오랫동안 포기하지 않고 매달려 준 학생들과 동료들에게 감사하다ˮ 라며 "마찰전기에 대한 미시적 이해를 통해, 보다 고효율 마찰전기 나노 발전기를 물질 수준에서 설계할 수 있게 됐으며, 실생활이나 산업에서 정전기를 제어하는 데 널리 이용되기를 바란다ˮ 라고 말했다.
한편 이번 연구는 한국연구재단의 자율운영 중점연구소 지원사업, SRC 이공분야기초연구사업, 미래소재디스커버리사업, 그리고 KAIST의 최장 30년까지 지원하는 그랜드 챌린지 30 사업의 지원을 받아 수행됐고, 관련 기술은 국내 특허출원이 완료됐다.
2022.05.26 조회수 15736 70년 만에 준-페르미 준위 분리 현상 제1 원리적으로 규명
국내 연구진이 70년 난제로 꼽히던 준-페르미 준위 분리 현상의 원자 수준 규명에 성공했다.
우리 대학 전기및전자공학부 김용훈 교수 연구팀이 반도체 소자 동작의 기원인 준-페르미 준위(quasi-Fermi level) 분리 현상을 제1 원리적으로 기술하는 데 최초로 성공했다고 27일 밝혔다.
제1 원리적인 방법이란 실험적 데이터나 경험적 모델을 사용하지 않고 슈뢰딩거 방정식을 직접 푸는 양자역학적 물질 시뮬레이션 방법이다.
김용훈 교수 연구팀의 연구 결과는 특히 비평형 상태의 나노 소자 내에서 발생하는 복잡한 전압 강하의 기원을 새로운 이론 체계와 슈퍼컴퓨터를 통해 규명함으로써, 다양한 첨단 반도체 소자의 분석 및 차세대 나노 소자 개발을 위한 이론적 틀을 제공할 것으로 기대되고 있다.
이주호 박사과정 학생이 제1 저자로 참여한 이번 연구 성과는 국제학술지 미국‘국립과학원회보(Proceedings of the National Academy of Sciences)’ 4월 23일 字 온라인판에 게재됐다. (논문명: Quasi-Fermi level splitting in nanoscale junctions from ab initio)
반도체 관련 교과서에도 소개되고 있는 준-페르미 준위 개념은 반도체 소자 내 전압인가 상황을 기술하는 표준적인 이론 도구로서 그동안 트랜지스터, 태양전지, 발광다이오드(LED) 등 다양한 반도체 소자들의 구동 원리를 이해하거나 성능을 결정하는데 경험적으로 사용돼왔다.
하지만 준-페르미 준위 분포 현상은 1956년 노벨 물리학상 수상자 윌리엄 쇼클리(William B. Shockley)가 제시한 지 70년이 지난 현재에도 전압 인가 상황의 반도체 소자 채널 내에서 측정을 하거나 계산을 해야 하는 어려움 때문에 원자 수준에서는 이해되지 못한 상황이 계속돼왔다.
연구팀은 차세대 반도체 소자의 후보군으로 주목을 받는 단일분자 소자에서, 나노미터 길이에서 발생하는 복잡한 전압 강하 현상을 최초로 규명해냈다. 특히 전도성이 강한 특정 나노 전자소자에 대해 비 선형적 전압 강하 현상이 일어나는 원인이 준-페르미 준위 분리 현상임을 밝혔다.
이러한 연구 성과는 김 교수 연구팀이 다년간에 걸쳐 새로운 반도체 소자 제1 원리 계산 이론을 확립하고 이를 소프트웨어적으로 구현했기에 가능했다. 이는 외산 소프트웨어에만 의존하던 반도체 설계 분야에서 세계적으로 경쟁력 있는 차세대 나노소자 전산 설계 원천기술을 확보했다는 점에서 큰 의미를 부여할 수 있다.
한편 이번 연구는 과학기술정보통신부 중견연구자지원사업, 나노소재원천기술개발사업, 기초연구실지원사업, 글로벌프론티어사업의 지원을 받아 수행됐다.
2020.04.27 조회수 18069
70년 만에 준-페르미 준위 분리 현상 제1 원리적으로 규명
국내 연구진이 70년 난제로 꼽히던 준-페르미 준위 분리 현상의 원자 수준 규명에 성공했다.
우리 대학 전기및전자공학부 김용훈 교수 연구팀이 반도체 소자 동작의 기원인 준-페르미 준위(quasi-Fermi level) 분리 현상을 제1 원리적으로 기술하는 데 최초로 성공했다고 27일 밝혔다.
제1 원리적인 방법이란 실험적 데이터나 경험적 모델을 사용하지 않고 슈뢰딩거 방정식을 직접 푸는 양자역학적 물질 시뮬레이션 방법이다.
김용훈 교수 연구팀의 연구 결과는 특히 비평형 상태의 나노 소자 내에서 발생하는 복잡한 전압 강하의 기원을 새로운 이론 체계와 슈퍼컴퓨터를 통해 규명함으로써, 다양한 첨단 반도체 소자의 분석 및 차세대 나노 소자 개발을 위한 이론적 틀을 제공할 것으로 기대되고 있다.
이주호 박사과정 학생이 제1 저자로 참여한 이번 연구 성과는 국제학술지 미국‘국립과학원회보(Proceedings of the National Academy of Sciences)’ 4월 23일 字 온라인판에 게재됐다. (논문명: Quasi-Fermi level splitting in nanoscale junctions from ab initio)
반도체 관련 교과서에도 소개되고 있는 준-페르미 준위 개념은 반도체 소자 내 전압인가 상황을 기술하는 표준적인 이론 도구로서 그동안 트랜지스터, 태양전지, 발광다이오드(LED) 등 다양한 반도체 소자들의 구동 원리를 이해하거나 성능을 결정하는데 경험적으로 사용돼왔다.
하지만 준-페르미 준위 분포 현상은 1956년 노벨 물리학상 수상자 윌리엄 쇼클리(William B. Shockley)가 제시한 지 70년이 지난 현재에도 전압 인가 상황의 반도체 소자 채널 내에서 측정을 하거나 계산을 해야 하는 어려움 때문에 원자 수준에서는 이해되지 못한 상황이 계속돼왔다.
연구팀은 차세대 반도체 소자의 후보군으로 주목을 받는 단일분자 소자에서, 나노미터 길이에서 발생하는 복잡한 전압 강하 현상을 최초로 규명해냈다. 특히 전도성이 강한 특정 나노 전자소자에 대해 비 선형적 전압 강하 현상이 일어나는 원인이 준-페르미 준위 분리 현상임을 밝혔다.
이러한 연구 성과는 김 교수 연구팀이 다년간에 걸쳐 새로운 반도체 소자 제1 원리 계산 이론을 확립하고 이를 소프트웨어적으로 구현했기에 가능했다. 이는 외산 소프트웨어에만 의존하던 반도체 설계 분야에서 세계적으로 경쟁력 있는 차세대 나노소자 전산 설계 원천기술을 확보했다는 점에서 큰 의미를 부여할 수 있다.
한편 이번 연구는 과학기술정보통신부 중견연구자지원사업, 나노소재원천기술개발사업, 기초연구실지원사업, 글로벌프론티어사업의 지원을 받아 수행됐다.
2020.04.27 조회수 18069